
前編では
| 波動光学の基本的な回折の定式化 | |
| 像形成 | |
| 光学系のシステム応答解析 |
について見てきた.
続編では
| 波面収差が存在する場合 | |
| 具体的な数値計算結果 |
を掲載する.
波面収差とは,波面がずれているときのそのズレ量をいう.
大気の歪みや光学系の取付誤差,焦点のズレなどで,波面収差が生じる.
ここでは波面収差の取り扱いと影響をまとめる.
例えば球面波を考える時,波面がずれていなければある球面上では位相はそろっている.
一方,波面収差が存在する場合は,ある球面上での位相がある分布を持っている.
つまり,波面収差とは,ある光路に対して位相ずれを付加したものともいえるので,射出瞳での波面収差分布を\(W(x,t)\)とすると瞳関数\(P\)を
\begin{align*} \mathcal{P}(x,y) &= P(x,y) e^{ikW(x,y)} \tag{5-1} \end{align*}という一般化瞳関数\(\mathcal{P}\)に置き換えればよい.
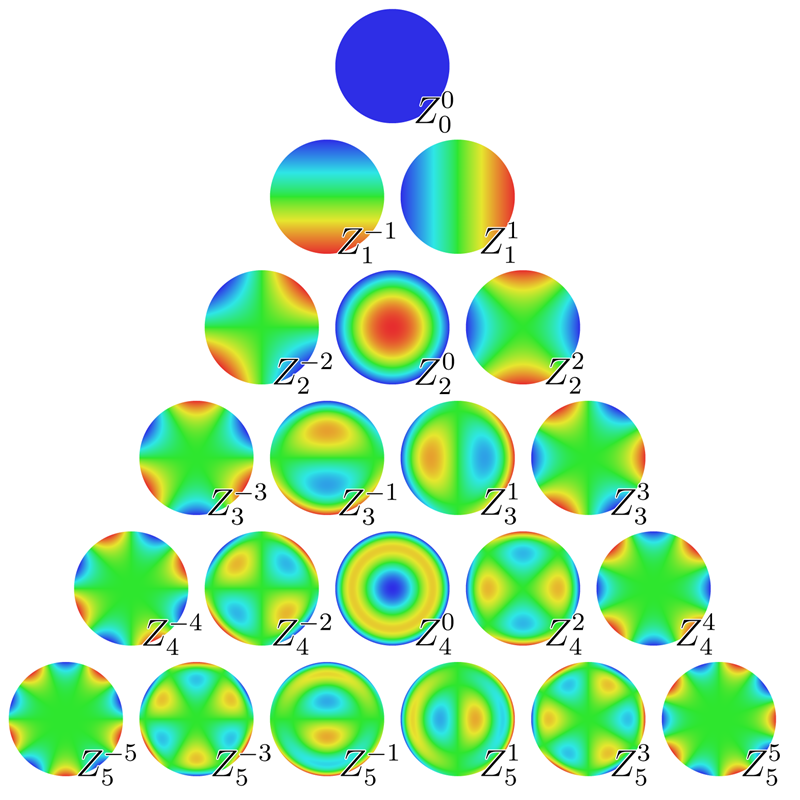
波面収差の近似のための基底関数として,Zernike多項式が広く用いられている.
Zernike多項式は極座標系の直交多項式であり,極座標系\((r,\theta)\)を\(0\leq r \leq 1\)と正規化しておくと,Zernike多項式\(Z_n^m\)は
\begin{alignat*}{2} & Z_{n}^{m}(r,\theta) && = \sqrt{2(n+1)} R_{n}^{m}(r) \begin{cases} \frac{1}{\sqrt{2}} & : m = 0 \\ \cos{(\left|m\right|\theta)} & : m > 0 \\ \sin{(\left|m\right|\theta)} & : m < 0 \end{cases} \tag{5-2} \\ & R_{n}^{\pm m}(r) && = \sum_{s=0}^{(n-m)/2} {\frac{(-1)^s (n-s)!}{s! (\frac{n+m}{2} - s)! (\frac{n-m}{2} - s)!} r^{n-2s}} \tag{5-3} \end{alignat*}と定義される.
すると波面収差\(W\)は
\begin{align*} W(x,y) &= \sum_{j=1}^J \alpha_j Z_j(r,\theta) \tag{5-4} \end{align*}と多項式近似でき,扱いが容易となる.
なお,厳密に波面収差を扱いたい場合は,光線追跡などの手法を用いて算出する.
下図はZernike多項式を可視化したものであり,わかりやすいところだと,たとえば\(Z_1^m\)はtiltずれを,\(Z_2^0\)はデフォーカスのずれを表現している.
波面収差がある場合,前編記事(4-11)式の瞳関数を一般化瞳関数へ置き換えて,ATFは
\begin{align*} H(f_x,f_y) &\propto P(-\lambda z_i f_x, -\lambda z_i f_y) e^{ikW(-\lambda z_i f_x, -\lambda z_i f_y)} \tag{5-5} \end{align*}となる.
つまり波面収差は位相歪みをもたらすことがわかる.
同様に前編記事(4-13)式の瞳関数を一般化瞳関数に書き換えると,波面収差がある場合のOTFは
\begin{align*} \mathcal{H}(f_x,f_y) &= \frac{\iint\limits_{-\infty}^{\infty} \mathcal{P}^{\ast}(x-\lambda z_i f_x,y-\lambda z_i f_y)\mathcal{P}(x,y)dxdy}{\iint\limits_{-\infty}^{\infty} \left|\mathcal{P}(x,y)\right|^2dxdq} \tag{5-6} \end{align*}となる.
シュバルツの不等式より,
\begin{align*} &\left|\mathcal{H}(f_x,f_y) \right|^2 \\ &= \quad \left| \frac{\iint\limits_{-\infty}^{\infty} \mathcal{P}^{\ast}(x-\lambda z_i f_x,y-\lambda z_i f_y)\mathcal{P}(x,y)dxdy}{\iint\limits_{-\infty}^{\infty} \left|\mathcal{P}(x,y)\right|^2dxdq} \right|^2 \\ &\leq \quad \frac{\iint\limits_{-\infty}^{\infty} \left|\mathcal{P}^{\ast}(x-\lambda z_i f_x,y-\lambda z_i f_y)\right|^2dxdy \iint\limits_{-\infty}^{\infty} \left|\mathcal{P}(x,y)\right|^2dxdy}{\left|\iint\limits_{-\infty}^{\infty} \left|P(x,y)\right|^2dxdq\right|^2} \\ &= \quad \frac{\iint\limits_{-\infty}^{\infty} \left|P^{\ast}(x-\lambda z_i f_x,y-\lambda z_i f_y)\right|^2dxdy \iint\limits_{-\infty}^{\infty} \left|P(x,y)\right|^2dxdy}{\left|\iint\limits_{-\infty}^{\infty} \left|P(x,y)\right|^2dxdq\right|^2} \\ &= \quad \left.\left|\mathcal{H}(f_x,f_y) \right|^2\right|_{W=0} \tag{5-7} \end{align*}となることから,波面収差はOTFの大きさを決して強めないことがわかる.
つまり,波面収差があると空間周波数成分のコントラストは低下する.
インコヒーレント系での単位インパルス応答であるPSFと,その周波数応答の絶対値であるMTFを実際に計算してみる.
SPFからはストレールレシオ(ここらへんも今度まとめようかな)という光学系の性能指標が計算されるし,
MTFは得られる画像の周波数成分,つまりどのくらい高解像度な画像が取得できるかなどの情報が得られる.
なお,ここでは光学系のパラメタ(波長\(\lambda\),焦点距離\(f\))は,
\begin{align*} \begin{aligned} \lambda & = 600\,\mathrm{nm} \\ f = z_i & = 5.0\,\mathrm{m} \\ \end{aligned} \tag{5-8} \end{align*}で固定した.
また,いかに載せる図は,開口瞳形状\(P\)(左上),MTF \(|\mathcal{H}|\)(左下),PSF \(s\) 2D(右上),PSF \(s\) 3D(右下)である.
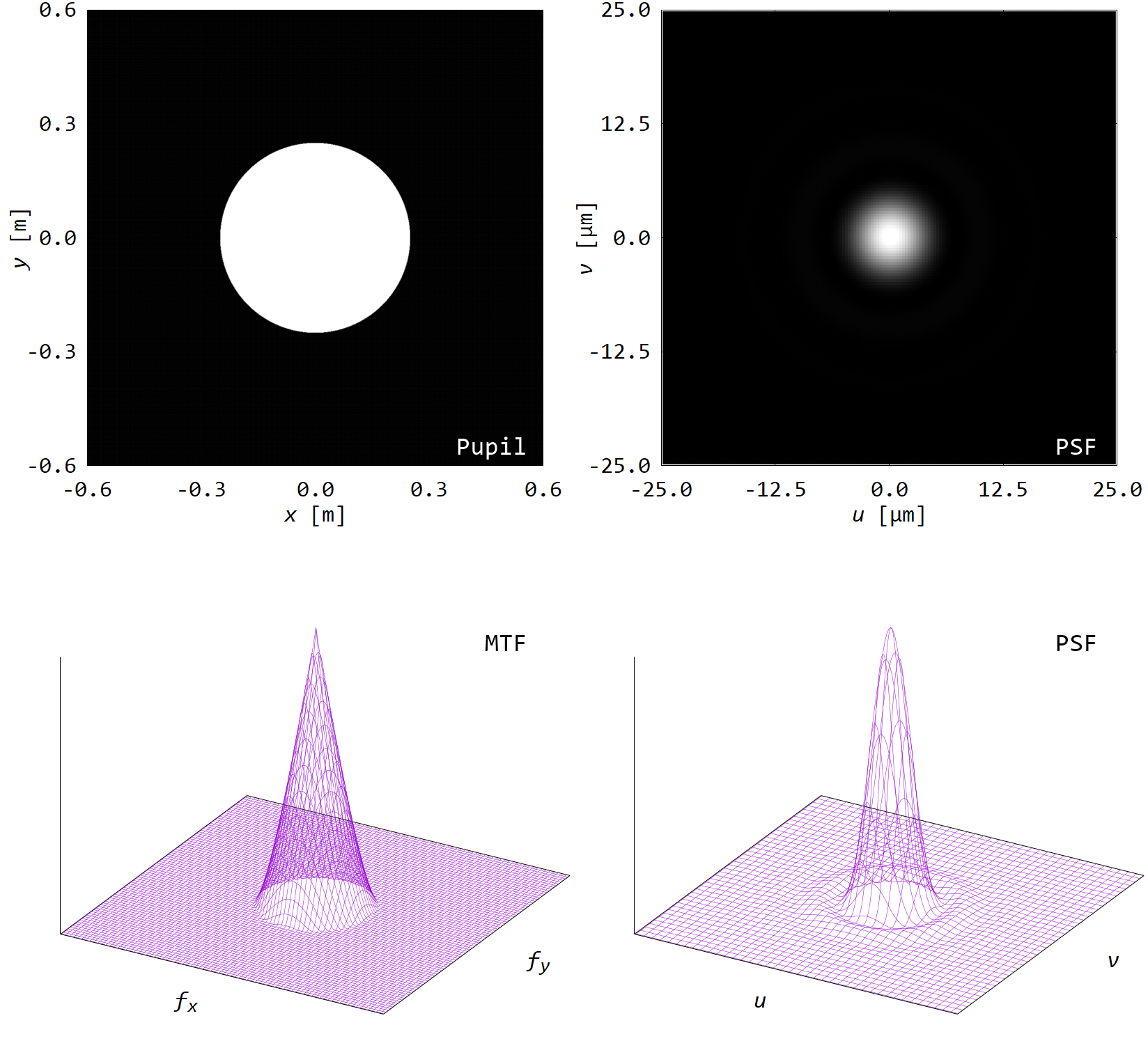
■ 基準(開口直径\(0.5\,\mathrm{m}\))
基準の開口形状は直径\(0.5\,\mathrm{m}\)円形形状である.
PSFをみると,理想状態であるにも関わらず,無限小点となっておらず広がっている.
これが幾何光学では扱えない回折現象であり,波動光学の持ち出す理由である.
なお,この円形開口による像をエアリーディスクという.
次にMTFをみる.
定常応答が最も高く,高周波に行くに従って応答が悪くなる.
なお,カットオフ周波数は開口直径を\(D\)とすると\(D/2\lambda z_i\)となる.
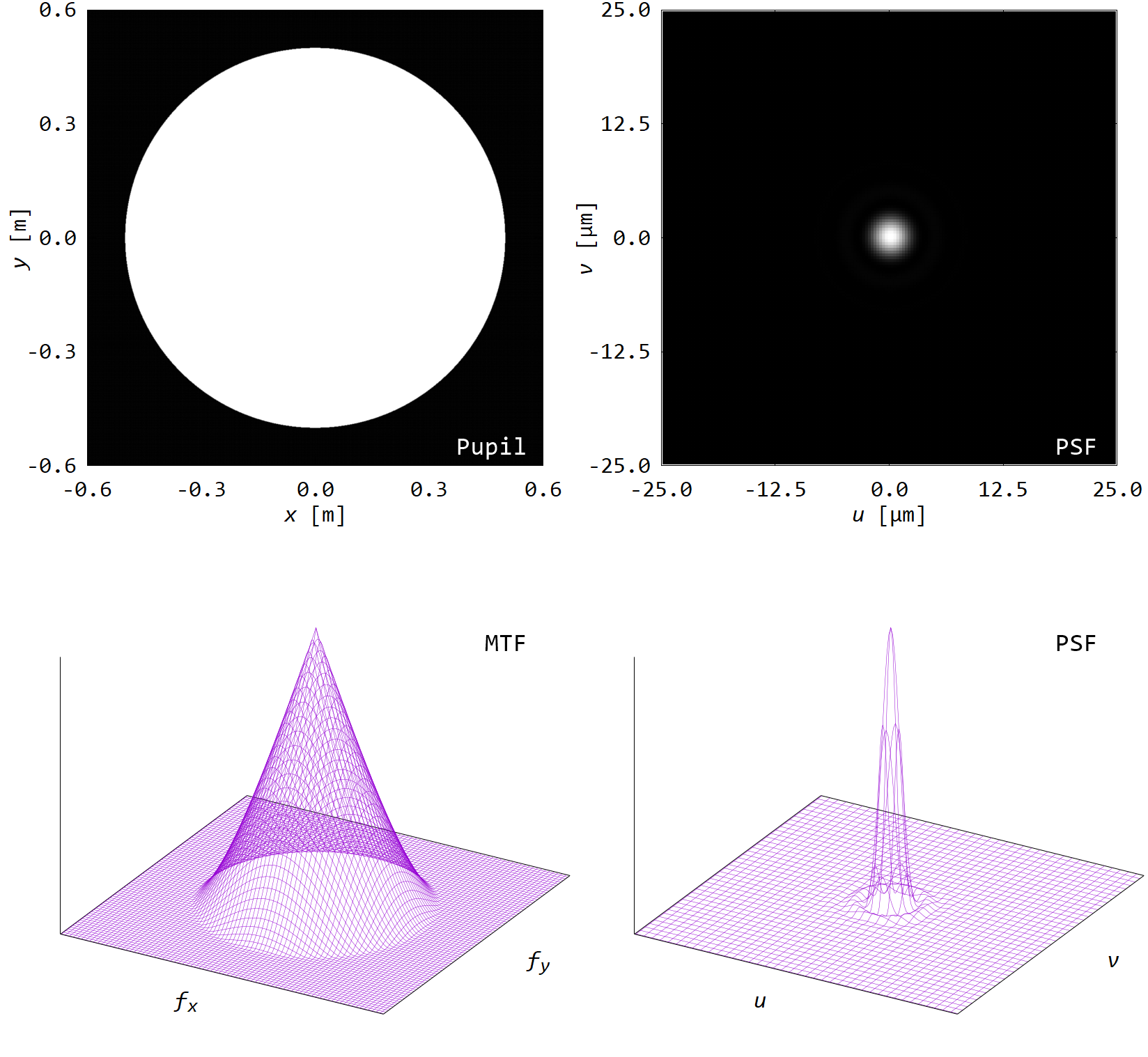
■ 開口径を倍に(開口直径\(1.0\,\mathrm{m}\))
開口径を倍にした.
するとPSFは小さくなり,MTFは広がる.
つまり,より高周波成分が撮像できるようになることを意味する.
望遠鏡の直径が大きい方がいいのはこのためである.
いくら露光時間を長くしてノイズを減らしたろころで,この回折現象は物理現象であるため,このPSFとりも高解像度な画像は得られない.
つまり,より遠くの,より小さいものを観測しようとするならば,開口経を大きくするほかないのである.
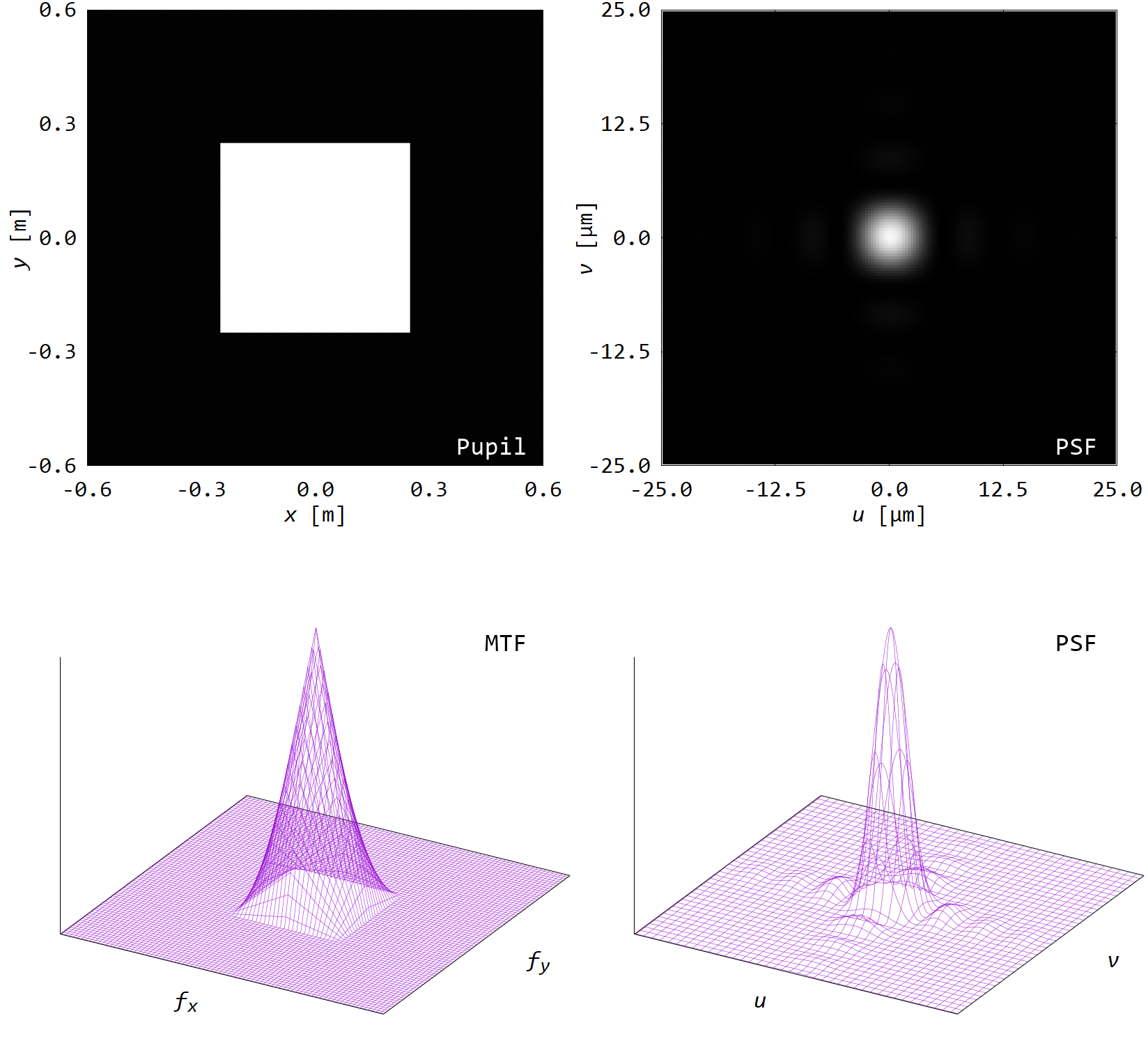
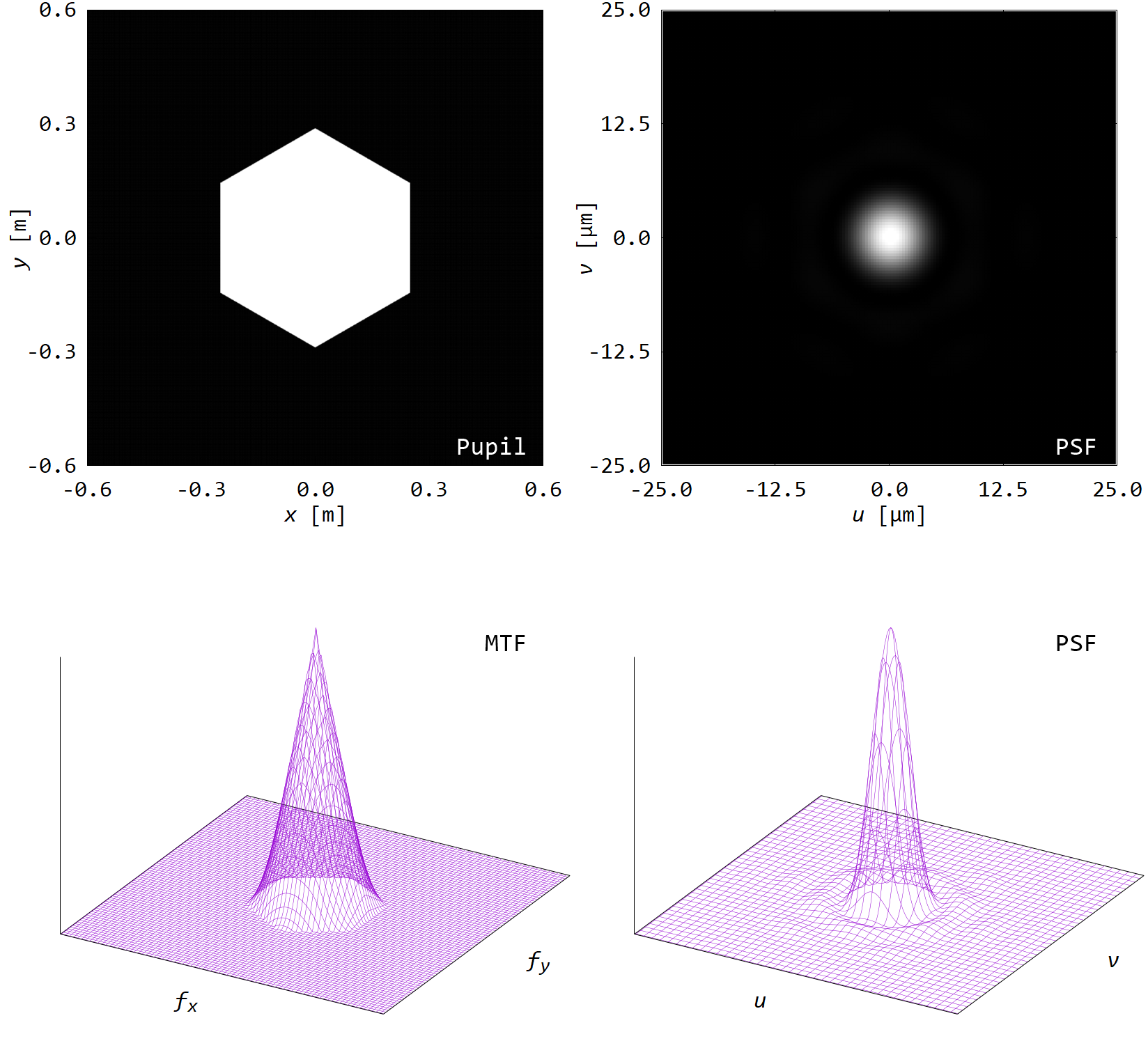
■ 開口形状を四角形,六角形に
開口形状を多角形にすると,PSFやMTF分布が対称ではなくなる.
そして,幅の小さい向きに強いサイドローブが発生する.
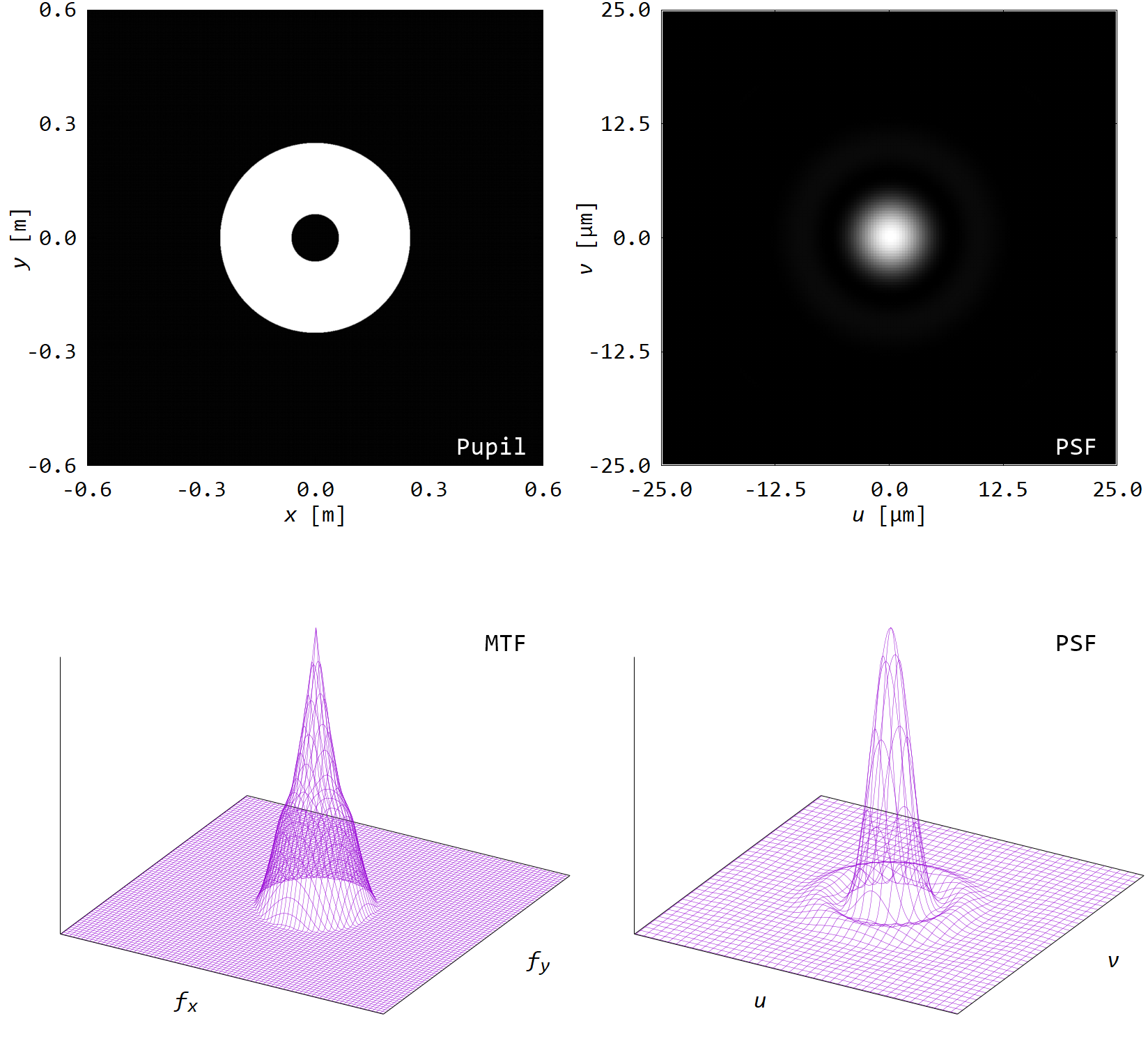
■ 中心に受光部用の穴を設置
反射望遠鏡などでは,主鏡で集めた光を副鏡で折り返し,主鏡中心部で撮像することがしばしばある.
その場合の開口瞳は下図のようになり,光学特性も単純円形開口より悪化する.
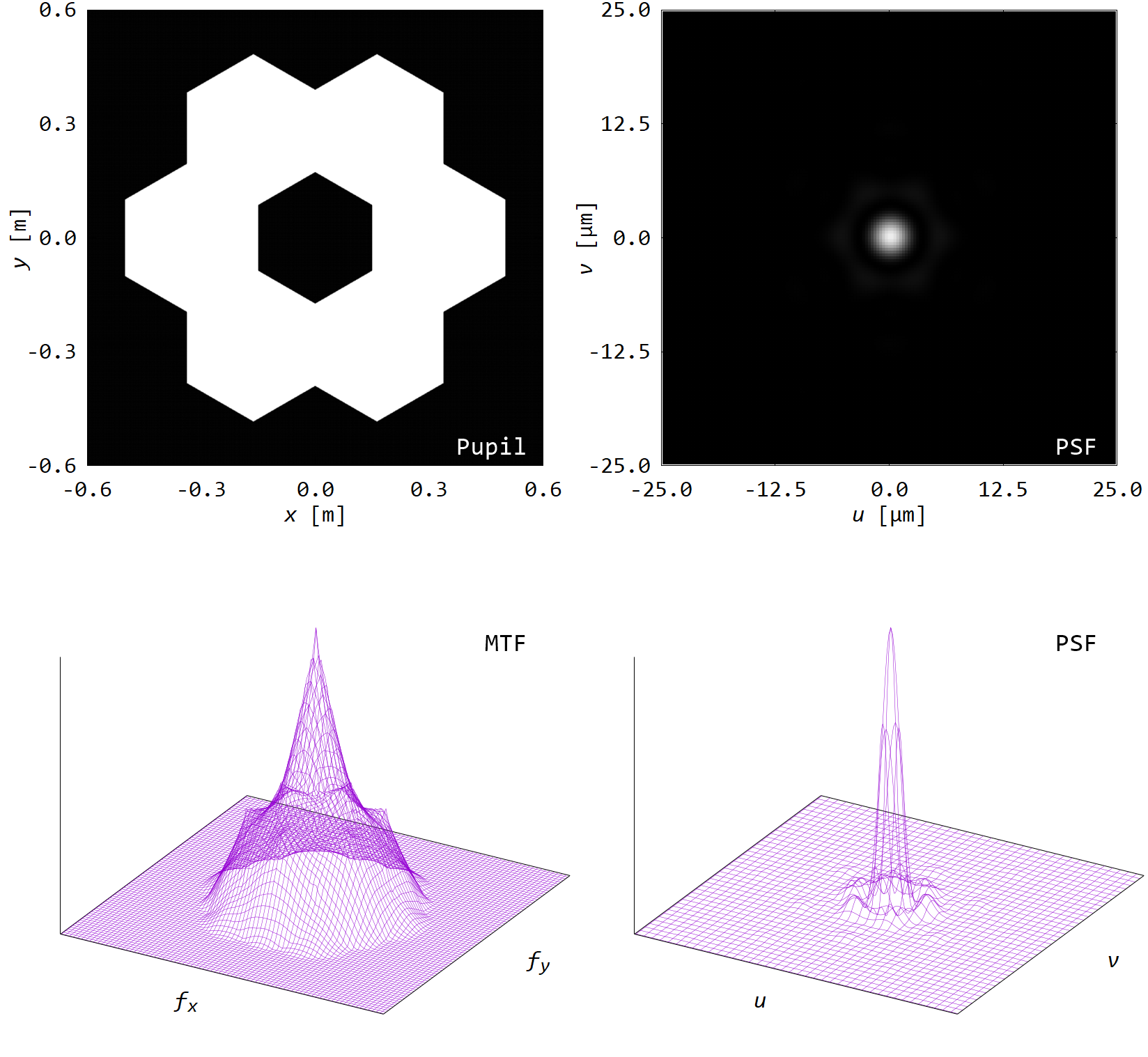
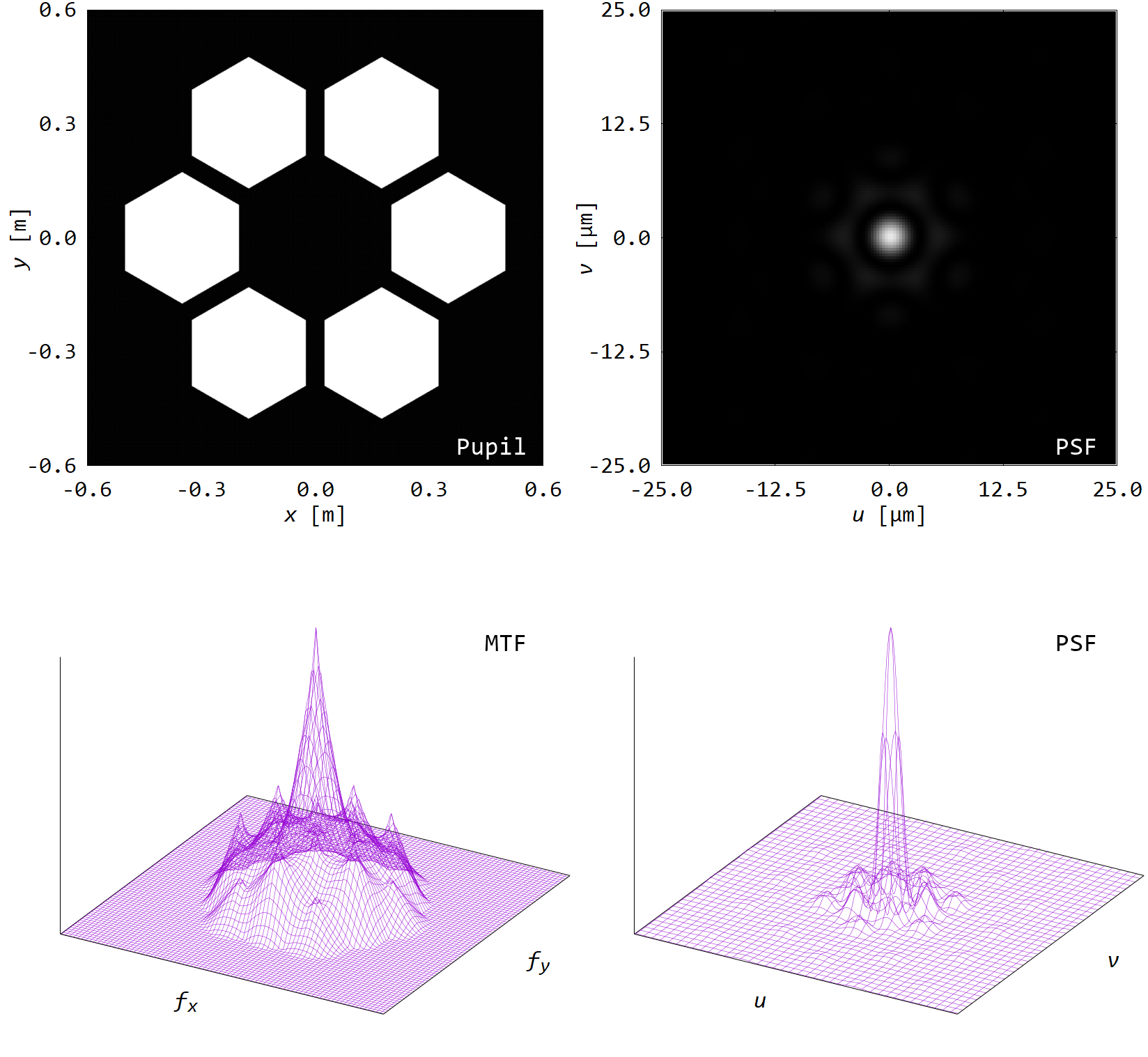
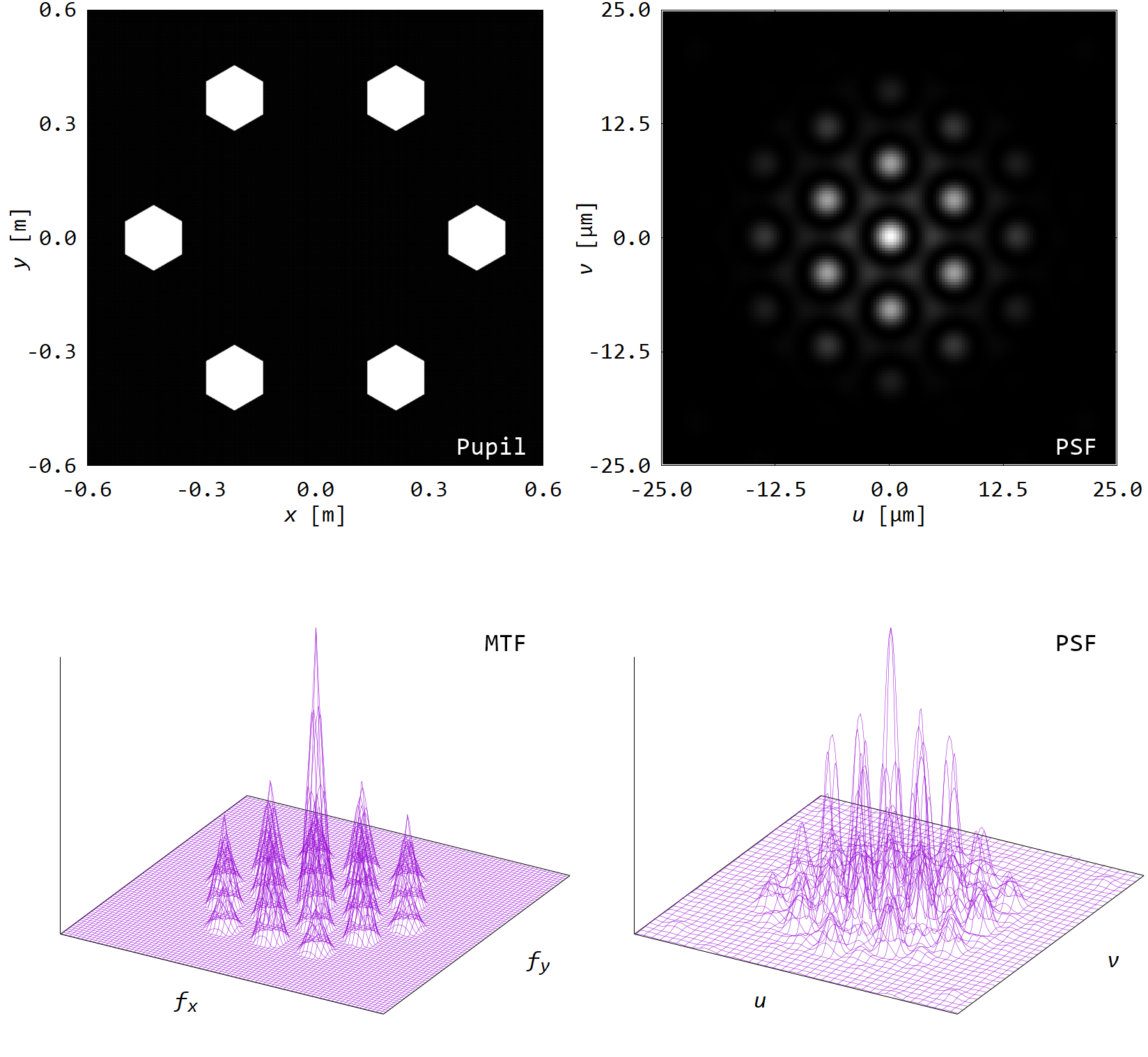
■ セグメント鏡
巨大な望遠鏡を建造する時,単一鏡で大きな主鏡をつくるのは難しい.
そこで,一般的にはいくつかの小さな鏡を組み合わせる.
その時,鏡の接合部のギャップが光学特性に影響を与える.
セグメント鏡(大)のように,ギャップが一定以上となるとMTFで0となる領域が生じる,つまり特定空間周波数が取得できなくなる.
これは,PSFの逆畳み込み演算によって,きれいな像が得られないことを意味する.
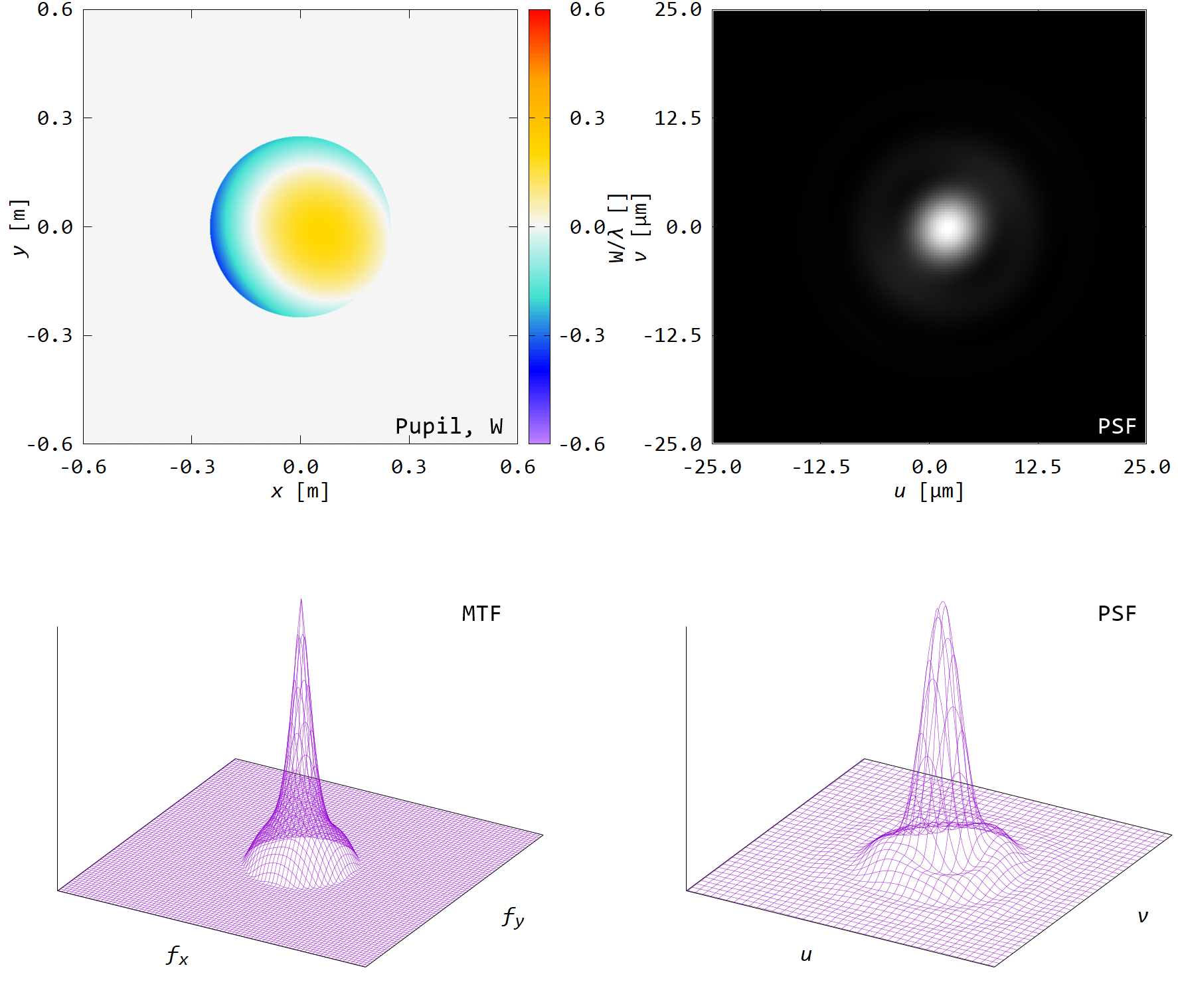
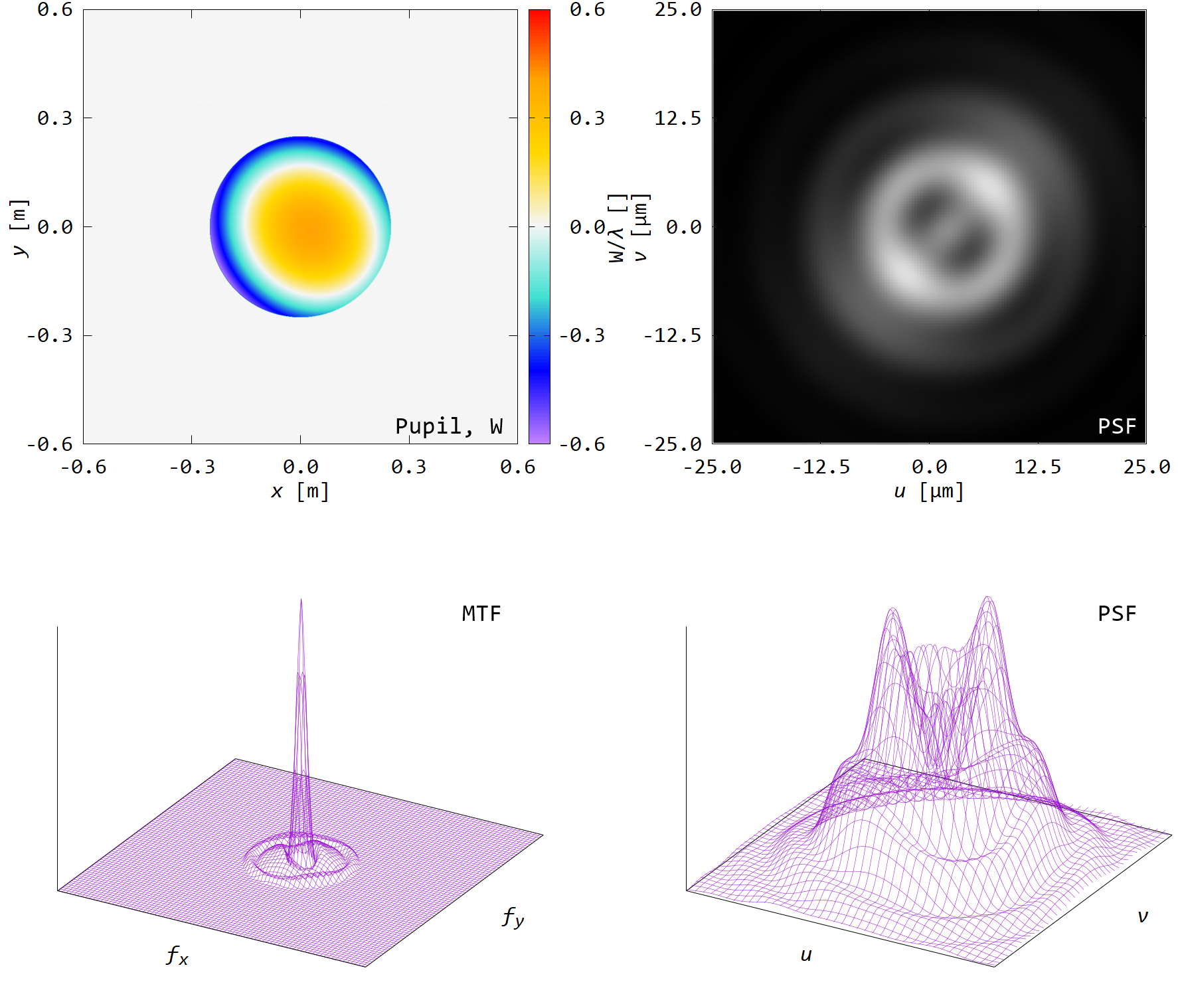
■ 円形開口
円形開口にZernike多項式で\(m \leq 2\)までの波面収差\(W\)をランダムに与えた.
下図のように,PSF形状は乱れ,MTFも悪化している.
ここでは示さないが,ストレールレシオもかなり低下している.
この光学系で撮像される像は,物体とこのPSF(点光源像,インパルス応答)との畳み込みであることを考えると,撮像される像も乱れることも想像できる(実際に適当な画像とコンボリューションとった画像,暇な時にでも計算してupします.).
実世界では,空気のゆれ,鏡の取付誤差,熱変性などによって波面収差が生じ,像が乱れる.
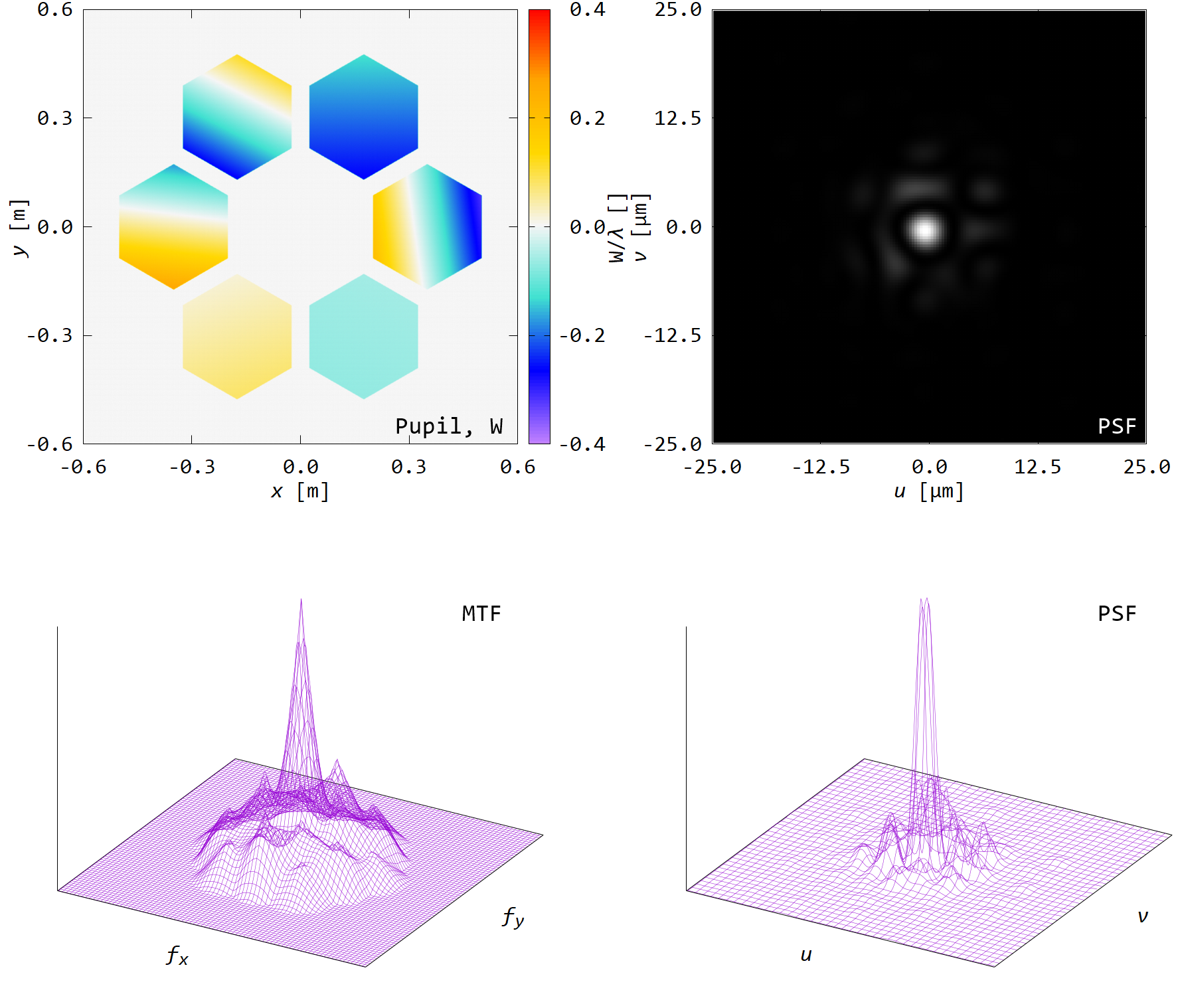
■ セグメント鏡(剛体)
次にセグメント鏡を例に取る.
ここでは先程とことなり,鏡面自体は剛体とし,その取付誤差\(x,y,z,\theta_x,\theta_y,\theta_z\)を与えた.
波長以下のずれしかなくとも,下図のようにPSFに大きな影響を与える.
(PSFの2D図だとわかりにくいが,よーくみると周りにゴーストが出ている.3D図でみるとさらにわかりやすい.)
PSF(インパルス応答)を求めたので,実際の像と畳み込みを行い,最終的なアウトプットも可視化して上げたい.
さらにはレイリー分解能やストレールレシオなどの光学系の性能指標もまとめたい.
そして,ここでは時不変,単色光を仮定したが,それも取り除いた理論も整理する.
名前
Email (※公開されることはありません)
コメント