０．注意

貧弱な自宅サーバーを使っているくせに，このページは重いgifアニメがたくさん貼り付けられています．

全て描画されるまで，しばらくお待ちください...．

１．はじめに

eeic （東京大学工学部電気電子・電子情報工学科） Advent Calendar，毎年毎年面白いですよね．

「航空宇宙工学アドベントカレンダーやりたい！」と前々から思っており，eeicの人間に，「eeicいいなぁ」って言ったところ，「航空宇宙でも作って」と言われてしまいました．

というわけで，昨日「東京大学航空宇宙工学科／専攻 Advent Calendar 2017」を立ち上げました．

 

立ち上げたはいいものの，1日で内容のある記事なんて書けぬ...．

そうだ！ 去年遊んだCFDまとめ直すか！

ということで，記念すべき航空宇宙アドベントカレンダー1つめは，CFD（数値流体力学 / Computational Fluid Dynamics）でのカルマン渦の再現と，その非対称性についての考察です．（圧倒的手抜き）

２．カルマン渦

カルマン渦とは，によると，

で，日本人ならば東シナ海に現れる雲のカルマン渦が天気予報の気象衛星画像に映り込むので馴染み深いだろう（以下のツイート参照）．

３．カルマン渦のCFD

解くべき方程式

まあ，簡単に行きましょう．

 

２次元非圧縮，外力，外部加熱なしを仮定する．

すると解くべき方程式は，

■ 連続の式（質量保存）

\begin{align*} \frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} & = 0 \tag{1} \end{align*}

■ ナビエ–ストークス方程式（運動量保存）

\begin{align*} \frac{\partial u}{\partial t} + u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y} & = - \frac{\partial p}{\partial x} + \frac{\mu}{\rho}\biggl(\frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2}\biggr) \tag{2} \\ \frac{\partial v}{\partial t} + u\frac{\partial v}{\partial x} + v\frac{\partial v}{\partial y} & = - \frac{\partial p}{\partial y} + \frac{\mu}{\rho}\biggl(\frac{\partial^2 v}{\partial x^2} + \frac{\partial^2 v}{\partial y^2}\biggr) \tag{3} \end{align*}

となる．

無次元化

非圧縮流れ，たとえば境界層方程式などでよくやる手法である，無次元をほどこす．

代表長さ\(L\)，\(x\)方向一様流速\(U\)，動圧\(\rho U^2\)で位置，速度，時間，圧力を以下のように無次元する．

\begin{align*} \left\{ \begin{alignedat}{1} x & \to \frac{x}{L} \\ u & \to \frac{u}{U} \\ t & \to \frac{t}{L/U} \\ p & \to \frac{p}{\rho U^2} \end{alignedat} \right. \tag{4} \end{align*}

すると解くべき方程式は

■ 連続の式（質量保存）

\begin{align*} \frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} & = 0 \tag{5} \end{align*}

■ ナビエ–ストークス方程式（運動量保存）

\begin{align*} \frac{\partial u}{\partial t} + u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y} & = - \frac{\partial p}{\partial x} + \frac{1}{\rm{Re}}\biggl(\frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2}\biggr) \tag{6} \\ \frac{\partial v}{\partial t} + u\frac{\partial v}{\partial x} + v\frac{\partial v}{\partial y} & = - \frac{\partial p}{\partial y} + \frac{1}{\rm{Re}}\biggl(\frac{\partial^2 v}{\partial x^2} + \frac{\partial^2 v}{\partial y^2}\biggr) \tag{7} \end{align*}

と無次元化される．

すると，単位系から解放されるとともに，方程式はレイノルズ数\(\rm{Re}\)

\begin{align*} {\rm{Re}} = \frac{\rho UL}{\mu} \tag{8} \end{align*}

というパラメタ１つで特徴づけされる．

つまり，たとえ物体の大きさや流速，密度などが異なった系だとしても，このレイノルズ数\(\rm{Re}\)が一致していれば流れは相似になる，ということだ．

 

これはとても強力で，たとえば航空機の翼まわりの空力的解析をしたい場合を考えよう．

実験室で航空機の速度の流れ（時速1000kmとか）を再現するのは難しい．

そこで，レイノルズ数が一致するように翼コード長（\(L\)に相当）が小さい翼を作って実験すれば，遅い流速でも解析したい航空機の翼と相似な流れが観測可能となるのだ．

数値計算のための式変形

あとは(5)~(7)を解けばいいだけですね！

と言ったものの，\(x,y,t\)の3次元空間で，独立変数\(u,v,p\)の3つ．

しんど...．

 

(6),(7)については，

\begin{align*} \frac{\partial u}{\partial t} & = - \frac{\partial p}{\partial x} + \frac{1}{\rm{Re}}\biggl(\frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2}\biggr) -\biggl(u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y}\biggr) \tag{6'} \\ \frac{\partial v}{\partial t} & = - \frac{\partial p}{\partial y} + \frac{1}{\rm{Re}}\biggl(\frac{\partial^2 v}{\partial x^2} + \frac{\partial^2 v}{\partial y^2}\biggr) -\biggl(u\frac{\partial v}{\partial x} + v\frac{\partial v}{\partial y}\biggr) \tag{7'} \end{align*}

とすれば，各独立変数の位置\(x,y\)での偏微分が求まってさえいれば，時間数値積分可能である．

 

(5)を用いてある時間\(t\)での独立変数\(u,v,p\)を求める方法を考える．

そのために，MAC法と呼ばれる，方程式を数値解法の存在するポアソン方程式へと帰着させる方法を用いる．

\(\frac{\partial}{\partial x}\)(6)\(+\)\(\frac{\partial}{\partial xy}\)(7)を，(5)よりいくつか項が消えることに注意しつつ計算すると，以下のようになる．

\begin{align*} \biggl(\frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2}\biggr)p &= - \Biggl\{ \biggl( \frac{\partial u}{\partial x} \biggr)^2 + \biggl( \frac{\partial v}{\partial y} \biggr)^2 + 2\frac{\partial u}{\partial y}\frac{\partial v}{\partial x} \Biggr\} - \frac{\partial D}{\partial t} \tag{9} \end{align*}

ただし，\(D\)は

\begin{align*} D & \equiv \frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} \to 0, \qquad \frac{\partial D}{\partial t} \simeq 0 \tag{10} \end{align*}

と，その時間微分項も消えるはずなのだが，数値計算の発散回避のために保持しておく．（CFDではこのようなTipsが多い．）

 

さてさて，(9)はMAC法によってめでたく\(p\)に関するポアソン方程式となった．

ポアソン方程式は，Jacobi法なり逐次緩和法（もしくはGauss–Seidel法）なりで解ける．

 

以上より，数値計算で解きやすい形へ変形することができた．

数値計算の方針

数値計算は，

	圧力場\(p(x,y)\)の計算 既知の速度場\(u(x,y),v(x,y)\)を用いて，\(p\)に関するポアソン方程式(9)を解き圧力場\(p(x,y)\)を求める．
	速度場\(u(x,y),v(x,y)\)の計算 得られた圧力場\(p(x,y)\)を用いて，(6'),(7')により次の時間ステップのステップ速度場\(u(x,y),v(x,y)\)を求める．（陽的Euler法）

を各時間ステップで繰り返せば良い．

数値計算のための離散化

さて，コンピュータシミュレーションでは離散化することが必須である．

(6')(7')(9)(10)を離散化していこう．

\(i\)は計算格子のインデックスである．

 

■ 勾配

単純に中心差分．

\begin{align*} \left.\frac{\partial f}{\partial x}\right|_i & \approx \frac{f_{i+1} - f_{i-1}}{2\varDelta x} \tag{11} \end{align*}

■ \(D\)の時間微分

未来はわからないので，普通に陽的Euler法

\begin{align*} \left.\frac{\partial D}{\partial t}\right|_t & \approx \frac{D_{t} - D_{t-1}}{\varDelta t} \tag{12} \end{align*}

■ 粘性項

これも中心差分．

\begin{align*} \left.\frac{\partial^2 f}{\partial x^2}\right|_i & \approx \frac{f_{i+1} -2f_{i} + f_{i-1}}{2\varDelta x^2} \tag{13} \end{align*}

■ 移流項

これは少し煩雑で，

\begin{align*} \left.u\frac{\partial f}{\partial x}\right|_i & \approx u_i \frac{-f_{i+2} +8\left(f_{i+1}-f_{i-1}\right) + f_{i-2}}{12\varDelta x} \\ \notag & \qquad\qquad + \left| u_i \right| \frac{f_{i+2} -4f_{i+1} +6f_{i} -4f_{i-1} +f_{i-2}}{4\varDelta x} \tag{14} \end{align*}

という4次精度の中心差分に\(\varDelta x^3 \left| u_i \right| \frac{\partial^4 f}{\partial x^4}\)の人工粘性を付加した3次精度の差分である，Kawamura–Kuwaharaスキームを用いる．

これはなどに詳しくのっている．

人工粘性について簡単に説明すると，これは4次以上の細かい関数\(f\)の変化に対して，それをカットする，つまりローパスフィルタのような役割を持った，仮想的な粘性項である．

さらに，Kawamura–Kuwaharaスキームでは差分を求める際の隣接する格子にかかる係数が風上の方が大きい，風上差分法（風上差分の物性値を重視する差分法）でもある．

座標系・計算条件

下図のような座標系\((x,y)\)をとる．

そして，原点に一辺が\(1\)の正方形障害物を設置．

レイノルズ数は\(\rm{Re}=70\)，

空間刻みは\(\varDelta x=\varDelta y=0.1\)，

時間刻みは\(\varDelta t=0.02\)（クーラン数に換算すると\(0.2\)）とした．

 

初期条件は\(u=1,v=0\)とし，

上流の境界条件は初期条件と同じ，その他の境界では線形外挿した．

座標系，障害物

４．結果

圧力場\(p(x,y)\)を可視化した結果は以下のgifアニメのようになる．

T_step=4000程度から，対称性が乱れ，カルマン渦が発生していることがわかる．

５．あれ？ ちょっとまてよ？

振動解

ここまで結果を出力して，ふと思うことがある．

「あれ？ なんで振動解（非対称解）が出現しているんだ？」

 

対称解も解である．また，振動解が解であることもわからないわけではない．

さらに，対称解より振動解の方が安定である，ということもわからないわけではない．

自然界では，外乱によってより安定な振動解で遷移しうる，ということもわからないわけではない．

 

ではなぜこの数値計算で非対称解である振動解への遷移が発生したのか？

考えられることは数値計算上の非対称性，つまり逐次緩和法と数値計算誤差である．

 

そこで，ポアソン方程式の解法を逐次緩和法からJacobi法に変更し，

さらに数値計算誤差が左右対称になるように，プログラム上の計算順を以下のように左右対称化した．

for (int i=0+1;i<=NX‐1;++i) {
  for (int j=0+1;j<=(NY/2);++j) {
    uy =   (U[i][j+1] ‐ U[i][j‐1]) / (2.0 * dy);
    rhsU[i][j] += (U[i][j+1] ‐ 2.0 * U[i][j] + U[i][j‐1]) / RE / (dy*dy);
  }
  for (int j=NY‐1;j>(NY/2);‐‐j) {
    uy = ‐ (U[i][j‐1] ‐ U[i][j+1]) / (2.0 * dy);
    rhsU[i][j] += (U[i][j‐1] ‐ 2.0 * U[i][j] + U[i][j+1]) / RE / (dy*dy);
  }
}

すると結果は以下のようになる．

逐次緩和法からJacobi法に変更

逐次緩和法からJacobi法に変更し，さらに計算順を対称化

Jacobi法に変更すると，カルマン渦の発生が遅れた．（対称解である時間が長くなった．）

また，数値計算計算誤差も対称解させた場合，振動解へと遷移することはなかった．（それはそう．）

振動解の増幅

以下の(15)で定義する，下流の点\((10,\pm 0)\)での左右の圧力差\(\varDelta p\)を可視化してみる．

\begin{align*} \varDelta p = \left| p(10,1) - p(10,-1) \right| \tag{15} \end{align*}

数値計算誤差も対称化させた場合は常に\(0\)なのは自明なので，逐次緩和法（Gauss–Seidel法）とJacobi法に関してプロットしてみた．

下流の点\((10,\pm 0)\)での左右の圧力差

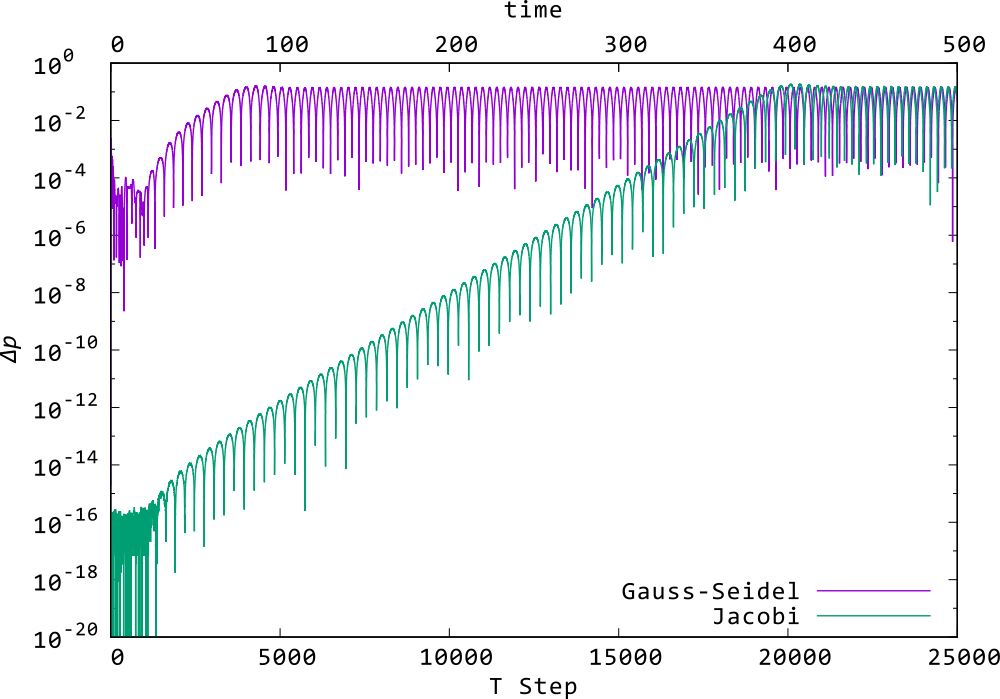
上図よりわかるのは，

	圧力差は初期より存在（カルマン渦としては現れていないが）
	圧力差は，指数関数的（片対数グラフで直線的）に増幅（計算方法によらず）
	圧力差が\(10^{-1}\)程度になると，カルマン渦として顕在化
	カルマン渦として顕在化した後は，増幅が停止し，安定

 

つまり，解いた方程式に左右の圧力差の増幅，一種のポジティブフィードバック的な作用が含まれていることが示唆される．

どこだ...？

\(\left| v \right|\)とかが怪しい？

 

しかし不思議であるのは，その増幅がある一定まで広がると停止することだ．

計算発散せずに，カルマン渦として安定してるので...．

 

流体力学，わからない...．

６．結論

対称な⽅程式よりカルマン渦という振動解（⾮対称解）が出現するのは，Gauss–Seidel法などの計算の⾮対称性，⾮対称な丸め誤差などの僅かな⾮対称成分が指数関数的に増幅され，不安定な対称解から安定な振動解へ遷移するためである．

実世界では，微⼩擾乱が⾮対称成分となると考えられる．

 

流体力学なにもわからん．

７．おわりに

航空宇宙の人間がみたら，ひと目で手抜きとわかる記事を書いてしまった．

次の記事はもう少しちゃんと書きます...．（予定）

８．出典

	Wikipedia. カルマン渦. Retrieved December 2, 2017, from https://ja.wikipedia.org/wiki/%E3%82%AB%E3%83%AB%E3%83%9E%E3%83%B3%E6%B8%A6
	東北大学 山本・佐野研究室. 第８章 実質微分の計算. Retrieved December 2, 2017, from http://www.caero.mech.tohoku.ac.jp/publicData/Daiguji/Chapter8.pdf

関連記事